Fixed Horizon


Fixed horizon labels is a classification labeling technique used in the following paper: Dixon, M., Klabjan, D. and Bang, J., 2016. Classification-based Financial Markets Prediction using Deep Neural Networks.

Note

Based on our industry experience, we would say this is by far the most popular technique for labeling data in financial machine learning.

Despite its numerous criticisms, this remains the go to choice for many practitioners. See Triple Barrier Labeling for an alternative approach.

Fixed time horizon is a common method used in labeling financial data, usually applied on time bars. The rate of return relative to \(t_0\) over time horizon \(h\), assuming that returns are lagged, is calculated as follows (M.L. de Prado, Advances in Financial Machine Learning, 2018):

\[r_{t0,t1} = \frac{p_{t1}}{p_{t0}} - 1\]

Where \(t_1\) is the time bar index after a fixed horizon has passed, and \(p_{t0}, p_{t1}\) are prices at times \(t_0, t_1\). This method assigns a label based on comparison of rate of return to a threshold \(\tau\)

\[\begin{split}\begin{equation} \begin{split} L_{t0, t1} = \begin{cases} -1 &\ \text{if} \ \ r_{t0, t1} < -\tau\\ 0 &\ \text{if} \ \ -\tau \leq r_{t0, t1} \leq \tau\\ 1 &\ \text{if} \ \ r_{t0, t1} > \tau \end{cases} \end{split} \end{equation}\end{split}\]

To avoid overlapping return windows, rather than specifying \(h\), the user is given the option of resampling the returns to get the desired return period. Possible inputs for the resample period can be found here.. Optionally, returns can be standardized by scaling by the mean and standard deviation of a rolling window. If threshold is a pd.Series, threshold.index and prices.index must match; otherwise labels will fail to be returned. If resampling is used, the threshold must match the index of prices after resampling. This is to avoid the user being forced to manually fill in thresholds.

The following shows the distribution of labels for standardized returns on closing prices of SPY in the time period from Jan 2008 to July 2016 using a 20-day rolling window for the standard deviation.

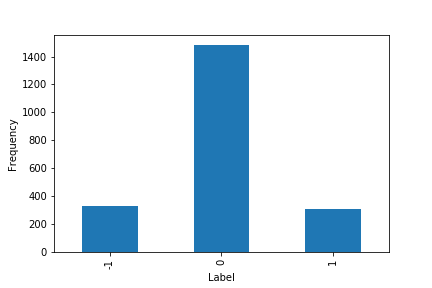
fixed horizon example

Distribution of labels on standardized returns on closing prices of SPY.

Though time bars are the most common format for financial data, there can be potential problems with over-reliance on time bars. Time bars exhibit high seasonality, as trading behavior may be quite different at the open or close versus midday; thus it will not be informative to apply the same threshold on a non-uniform distribution. Solutions include applying the fixed horizon method to tick or volume bars instead of time bars, using data sampled at the same time every day (e.g. closing prices) or inputting a dynamic threshold as a pd.Series corresponding to the timestamps in the dataset. However, the fixed horizon method will always fail to capture information about the path of the prices [Lopez de Prado, 2018].

Note

Underlying Literature

The following sources describe this method in more detail:

Implementation

Chapter 3.2 Fixed-Time Horizon Method, in Advances in Financial Machine Learning, by M. L. de Prado.

Work “Classification-based Financial Markets Prediction using Deep Neural Networks” by Dixon et al. (2016) describes how labeling data this way can be used in training deep neural networks to predict price movements.

fixed_time_horizon(prices, threshold=0, resample_by=None, lag=True, standardized=False, window=None)

Fixed-Time Horizon Labeling Method.

Originally described in the book Advances in Financial Machine Learning, Chapter 3.2, p.43-44.

Returns 1 if return is greater than the threshold, -1 if less, and 0 if in between. If no threshold is provided then it will simply take the sign of the return.

Parameters:

  • prices – (pd.Series or pd.DataFrame) Time-indexed stock prices used to calculate returns.

  • threshold – (float or pd.Series) When the absolute value of return exceeds the threshold, the observation is labeled with 1 or -1, depending on the sign of the return. If return is less, it’s labeled as 0. Can be dynamic if threshold is inputted as a pd.Series, and threshold.index must match prices.index. If resampling is used, the index of threshold must match the index of prices after resampling. If threshold is negative, then the directionality of the labels will be reversed. If no threshold is provided, it is assumed to be 0 and the sign of the return is returned.

  • resample_by –

    (str) If not None, the resampling period for price data prior to calculating returns. ‘B’ = per business day, ‘W’ = week, ‘M’ = month, etc. Will take the last observation for each period. For full details see here.

  • lag – (bool) If True, returns will be lagged to make them forward-looking.

  • standardized – (bool) Whether returns are scaled by mean and standard deviation.

  • window – (int) If standardized is True, the rolling window period for calculating the mean and standard deviation of returns.

Returns:

(pd.Series or pd.DataFrame) -1, 0, or 1 denoting whether the return for each observation is less/between/greater than the threshold at each corresponding time index. First or last row will be NaN, depending on lag.

Example

Below is an example on how to use the Fixed Horizon labeling technique on real data.

# Import packages
import pandas as pd
import numpy as np
import yfinance as yf

# Import MlFinLab tools
from mlfinlab.labeling.fixed_time_horizon import fixed_time_horizon

# Loading SPY data close prices
data = yf.download(tickers="SPY", start="2008-01-01", end="2016-01-01", interval="1d")[
    "Adj Close"
]

# Create a series of random thresholds - used to dynamically set the threshold
custom_threshold = pd.Series(np.random.random(len(data)) / 100, index=data.index)

# Create labels
labels = fixed_time_horizon(prices=data, threshold=0.01, lag=True)

# Create labels with a dynamic threshold
labels = fixed_time_horizon(prices=data, threshold=custom_threshold, lag=True)

# Create labels with standardization
labels = fixed_time_horizon(
    prices=data, threshold=1, lag=True, standardized=True, window=5
)

# Create labels after resampling weekly with standardization
labels = fixed_time_horizon(
    prices=data, threshold=1, resample_by="W", lag=True, standardized=True, window=4
)

Research Notebook

The following research notebook can be used to better understand the Fixed Horizon labeling technique.

  • Fixed Horizon Example

Presentation Slides


References