Note
The following implementation and documentation is based on the work of F. Musciotto, L. Marotta, S. Miccichè, and R. N. Mantegna Bootstrap validation of links of a minimum spanning tree.
Bootstrapping
Bootstrapping is a statistical method used to resample a dataset with replacement to estimate its population statistics (such as mean, median, standard deviation, etc.) In machine learning applications, bootstrap sampling usually leads to less overfitting and improvement of the stability of our models. Bootstrap methods draw small samples (with replacement) from a large dataset one at a time, and organizing them to construct a new dataset. Here we examine three bootstrap methods. Row, Pair, and Block Bootstrap.
Note
Underlying Literature
The following sources elaborate extensively on the topic:
-
Bootstrap validation of links of a minimum spanning tree by Musciotto, F., Marotta, L., Miccichè, S. and Mantegna, R.N.
Row Bootstrap
The Row Bootstrap method samples rows with replacement from a dataset to generate a new dataset. For example, for a dataset of size \(T \times n\) which symbolizes \(T\) rows (timesteps) and \(n\) columns (assets), if we use the row bootstrap method to generate a new matrix of the same size, we sample with replacement \(T\) rows to form the new dataset. This implies that the new dataset can contain repeated data from the original dataset.

(Left) Original dataset of size \(T \times n\). (Right) Row bootstrap dataset of size \(T \times n\).
Implementation
- row_bootstrap(mat, n_samples=1, size=None)
-
Uses the Row Bootstrap method to generate a new matrix of size equal or smaller than the given matrix.
It samples with replacement a random row from the given matrix. If the required bootstrapped columns’ size is less than the columns of the original matrix, it randomly samples contiguous columns of the required size. It cannot generate a matrix greater than the original.
It is inspired by the following paper: Musciotto, F., Marotta, L., Miccichè, S. and Mantegna, R.N., 2018. Bootstrap validation of links of a minimum spanning tree. Physica A: Statistical Mechanics and its Applications, 512, pp.1032-1043..
- Parameters:
-
-
mat – (pd.DataFrame/np.array) Matrix to sample from.
-
n_samples – (int) Number of matrices to generate.
-
size – (tuple) Size of the bootstrapped matrix.
-
- Returns:
-
(np.array) The generated bootstrapped matrices. Has shape (n_samples, size[0], size[1]).
Example
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
from mlfinlab.data_generation.bootstrap import row_bootstrap
# Create random matrix
original_dataset = np.random.rand(15, 6)
# Generate a row bootstrap matrix
bootstrap_dataset = row_bootstrap(original_dataset, n_samples=1)
# Plot them
fig, axes = plt.subplots(1, 2)
sns.heatmap(original_dataset, annot=True, fmt=".2f", ax=axes[0])
axes[0].set_title("Original Dataset")
sns.heatmap(bootstrap_dataset[0], annot=True, fmt=".2f", ax=axes[1])
axes[1].set_title("Row Bootstrap Dataset")
plt.show()
Pair Bootstrap
The Pair Bootstrap method samples pairs of columns with replacement from a dataset to generate a new dataset. This new dataset can be used to generate a dependence matrix, as is a correlation matrix. For example, for a dataset of size \(T \times n\) which symbolizes \(T\) rows (timesteps) and \(n\) columns (assets), if we use the pair bootstrap method to generate a correlation matrix of size \(n \times n\), we iterate over the upper triangular indices of the correlation matrix. For each index, we sample with replacement 2 columns and all their rows. We calculate the correlation measure of this pair and use it to fill the given index of the correlation matrix. We repeat this process until we fill the correlation matrix.

(Left) Original dataset of size \(T \times n\). (Right) Row bootstrap dataset, each of size \(T \times 2\). Each pair dataset can be used to generate a dependence matrix (e.g. correlation matrix).
Implementation
- pair_bootstrap(mat, n_samples=1, size=None)
-
Uses the Pair Bootstrap method to generate a new correlation matrix of returns.
It generates a correlation matrix based on the number of columns of the returns matrix given. It samples with replacement a pair of columns from the original matrix, the rows of the pairs generate a new row-bootstrapped matrix. The correlation value of the pair of assets is calculated and its value is used to fill the corresponding value in the generated correlation matrix.
It is inspired by the following paper: Musciotto, F., Marotta, L., Miccichè, S. and Mantegna, R.N., 2018. Bootstrap validation of links of a minimum spanning tree. Physica A: Statistical Mechanics and its Applications, 512, pp.1032-1043..
- Parameters:
-
-
mat – (pd.DataFrame/np.array) Returns matrix to sample from.
-
n_samples – (int) Number of matrices to generate.
-
size – (int) Size of the bootstrapped correlation matrix.
-
- Returns:
-
(np.array) The generated bootstrapped correlation matrices. Has shape (n_samples, mat.shape[1], mat.shape[1]).
Example
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
from mlfinlab.data_generation.bootstrap import pair_bootstrap
# Create random matrix
original_dataset = np.random.rand(50, 10)
# Generate a pair bootstrap correlation matrix
bootstrap_corr_matrix = pair_bootstrap(original_dataset, n_samples=1)
# Plot them
fig, axes = plt.subplots(1, 2)
sns.heatmap(pd.DataFrame(original_dataset).corr(), ax=axes[0])
axes[0].set_title("Original Dataset")
sns.heatmap(bootstrap_corr_matrix[0], ax=axes[1])
axes[1].set_title("Pair Bootstrap Dataset")
plt.show()
Block Bootstrap
The Block Bootstrap method samples blocks of data with replacement from a dataset to generate a new dataset. The block size can be of a size equal to or less than the original dataset. The blocks in this module are non-overlapping (except on the edges of the dataset if the blocks cannot perfectly split the data). Their ideal size depends on the data and its application. For example, for a dataset of size \(T \times n\) which symbolizes \(T\) rows (timesteps) and \(n\) columns (assets), if we use the Block Bootstrap method to split the data set into blocks of \(2 \times 2\), then we sample as many blocks as needed to fill the bootstrapped matrix.
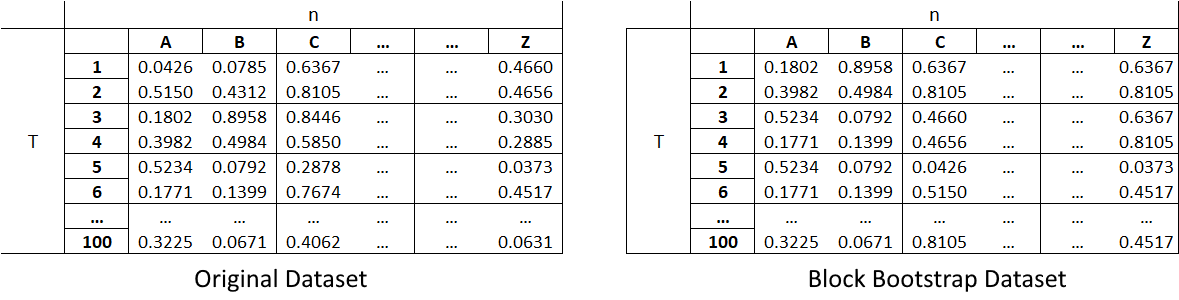
(Left) Original dataset of size \(T \times n\). (Right) Block bootstrap dataset of size \(T \times n\) created with blocks of size \(2 \times 2\).
Implementation
- block_bootstrap(mat, n_samples=1, size=None, block_size=None)
-
Uses the Block Bootstrap method to generate a new matrix of size equal to or smaller than the given matrix.
It divides the original matrix into blocks of the given size. It samples with replacement random blocks to populate the bootstrapped matrix. It cannot generate a matrix greater than the original.
It is inspired by the following paper: Künsch, H.R., 1989. The jackknife and the bootstrap for general stationary observations. Annals of Statistics, 17(3), pp.1217-1241..
- Parameters:
-
-
mat – (pd.DataFrame/np.array) Matrix to sample from.
-
n_samples – (int) Number of matrices to generate.
-
size – (tuple) Size of the bootstrapped matrix.
-
block_size – (tuple) Size of the blocks.
-
- Returns:
-
(np.array) The generated bootstrapped matrices. Has shape (n_samples, size[0], size[1]).
Example
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
from mlfinlab.data_generation.bootstrap import block_bootstrap
# Create random matrix
original_dataset = np.random.rand(14, 9)
# Generate a block bootstrap matrix
bootstrap_dataset = block_bootstrap(original_dataset, n_samples=1, block_size=(2, 3))
# Plot them
fig, axes = plt.subplots(1, 2, figsize=(9, 5))
sns.heatmap(original_dataset, annot=True, fmt=".2f", ax=axes[0])
axes[0].set_title("Original Dataset")
sns.heatmap(bootstrap_dataset[0], annot=True, fmt=".2f", ax=axes[1])
axes[1].set_title("Block Bootstrap Dataset")
plt.show()
Research Notebook
The following research notebook can be used to better understand the bootstrap methods.
-
Generating Matrices using Bootstrap Methods