Hierarchical Correlation Block Model (HCBM)
Note
The following implementation and documentation closely follow the work of Marti, Andler, Nielsen, and Donnat: Clustering financial time series: How long is enough?.
HCBM
According to the research paper, it has been verified that price time series of traded assets for different markets exhibit a hierarchical correlation structure. Another property they exhibit is the non-Gaussianity of daily asset returns. These two properties prompt the use of alternative correlation coefficients, with the most used correlation coefficient is the Pearson correlation coefficient, and the definition of the Hierarchical Correlation Block Model (HCBM).
Warning
Pearson correlation only captures linear effects. If two variables have strong non-linear dependency (squared or abs for example) Pearson correlation won’t find any pattern between them. For information about capturing non-linear dependencies, read our Introduction to Codependence.
The HCBM model consists of correlation matrices having a hierarchical block structure. Each block corresponds to a correlation cluster. The HCBM defines a set of nested partitions \(P = \{P_0 \supseteq P_1 \supseteq ... \supseteq P_h\}\) for some \(h \in [1, N]\) for \(N\) univariate random variables. Each partition is further subdivided and partitioned again for \(k\) levels where \(1 \leq k \leq h\). We define \(\underline{\rho_k}\) and \(\bar{\rho_k}\) such that for all \(1 \leq i,j \leq N\), we have \(\underline{\rho_k} \leq \rho_{i,j} \leq \bar{\rho_k}\), when \(C^{(k)}(X_i) = C^{(k)}(X_j)\) and \(C^{(k+1)}(X_i) \neq C^{(k+1)}(X_j)\) (\(C^{(k)}(X_i)\) denotes the cluster \(X_i\) in partition \(P_k\)).
This implies that \(\underline{\rho_k}\) and \(\bar{\rho_k}\) are the minimum and maximum correlation factors respectively within all clusters \(C^{(k)}_i\) in the partition \(P_k\) at depth \(k\). In order for the generated matrix to have a proper nested correlation hierarchy, we must have \(\bar{\rho_k} < \underline{\rho_{k+1}}\) hold true for all \(k\).
Figure 1 is a sample HCBM matrix generated with \(N = 256\), \(k = 4\), \(h = 4\), \(\underline{\rho_k} = 0.1\), and \(\bar{\rho_k} = 0.9\).
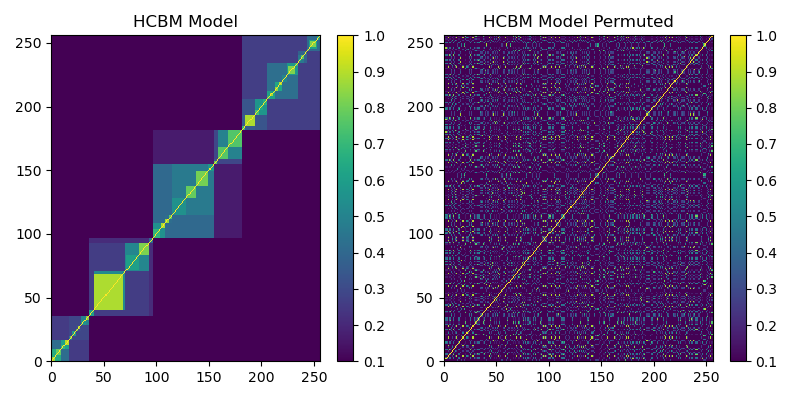
Figure 1. (Left) HCBM matrix. (Right) Left HCBM matrix permuted once.
Figure 1 shows how an HCBM matrix has different levels of hierarchical clusters. The picture on the right shows how a correlation matrix is most commonly observed from asset returns.
Implementation
- generate_hcmb_mat(t_samples, n_size, rho_low=0.1, rho_high=0.9, blocks=4, depth=4, permute=False)
-
Generates a Hierarchical Correlation Block Model (HCBM) matrix of correlation values.
By using a uniform distribution we select the start and end locations of the blocks in the matrix. For each block, we recurse depth times and repeat splitting up the sub-matrix into blocks. Each depth level has a unique correlation (rho) values generated from a uniform distributions, and bounded by rho_low and rho_high.
It is reproduced with modifications from the following paper: Marti, G., Andler, S., Nielsen, F. and Donnat, P., 2016. Clustering financial time series: How long is enough?. arXiv preprint arXiv:1603.04017.
- Parameters:
-
-
t_samples – (int) Number of HCBM matrices to generate.
-
n_size – (int) Size of HCBM matrix.
-
rho_low – (float) Lower correlation bound of the matrix. Must be greater or equal to 0.
-
rho_high – (float) Upper correlation bound of the matrix. Must be less or equal to 1.
-
blocks – (int) Number of blocks to generate per level of depth.
-
depth – (int) Depth of recursion for generating new blocks.
-
permute – (bool) Whether to permute the final HCBM matrix.
-
- Returns:
-
(np.array) Generated HCBM matrix of shape (t_samples, n_size, n_size).
Example
import matplotlib.pyplot as plt
from mlfinlab.data_generation.hcbm import generate_hcmb_mat
# Initialize parameters.
samples = 4
dim = 200
rho_low = 0.1
rho_high = 0.9
# Generate HCBM matrices.
hcbm_mats = generate_hcmb_mat(t_samples=samples,
n_size=dim,
rho_low=rho_low,
rho_high=rho_high)
# Plot them.
for i in range(len(hcbm_mats)):
plt.subplot(2, 2, i + 1)
plt.pcolormesh(hcbm_mats[i], cmap='viridis')
plt.colorbar()
plt.show()
Time Series Generation from HCBM Matrix
To generate financial time series models from HCBM matrices we will consider two models.
-
The standard, but not entirely accurate, gaussian random walk model. Its increments are realization from a \(N\)-variate Gaussian \(X \sim N(0, \Sigma)\)
-
The \(N\)-variate Student’s t-distribution, with degree of freedom \(v = 3\), \(X \sim t_v(0, \frac{v-2}{v}\Sigma)\)
The advantage of using the \(N\)-variate Student’s t-distribution is that it captures heavy-tailed behavior and tail-dependence. The authors assert that “It has been shown that this distribution (Student’s t-distribution) yields a much better fit to real returns than the Gaussian distribution”
Both distributions are parameterized by a covariance matrix \(\Sigma\). We define \(\Sigma\) such that the underlying correlation matrix has a HCBM structure as shown in Figure 1.
Figure 2 shows both distributions created from an HCBM matrix. It has 1000 samples
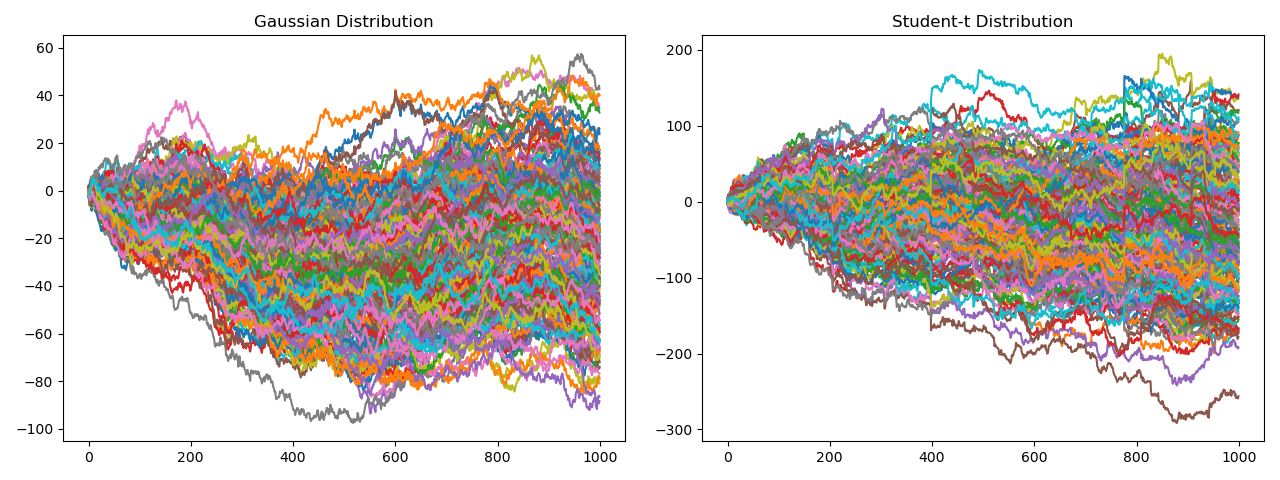
Figure 2. (Left) Time Series generated from a Gaussian Distribution. (Right) Time Series generated from a Student-t distribution.
Implementation
- time_series_from_dist(corr, t_samples=1000, dist='normal', deg_free=3)
-
Generates a time series from a given correlation matrix.
It uses multivariate sampling from distributions to create the time series. It supports normal and student-t distributions. This method relies and acts as a wrapper for the np.random.multivariate_normal and statsmodels.sandbox.distributions.multivariate.multivariate_t_rvs modules. https://numpy.org/doc/stable/reference/random/generated/numpy.random.multivariate_normal.html https://www.statsmodels.org/stable/sandbox.html?highlight=sandbox#module-statsmodels.sandbox
It is reproduced with modifications from the following paper: Marti, G., Andler, S., Nielsen, F. and Donnat, P., 2016. Clustering financial time series: How long is enough?. arXiv preprint arXiv:1603.04017.
- Parameters:
-
-
corr – (np.array) Correlation matrix.
-
t_samples – (int) Number of samples in the time series.
-
dist – (str) Type of distributions to use. Can take the values [“normal”, “student”].
-
deg_free – (int) Degrees of freedom. Only used for student-t distribution.
-
- Returns:
-
(pd.DataFrame) The resulting time series of shape (len(corr), t_samples).
Example
import matplotlib.pyplot as plt
from mlfinlab.data_generation.hcbm import generate_hcmb_mat, time_series_from_dist
# Initialize parameters
samples = 1
dim = 200
rho_low = 0.1
rho_high = 0.9
# Generate time series from HCBM matrix
hcbm_mats = generate_hcmb_mat(t_samples=samples,
n_size=dim,
rho_low=rho_low,
rho_high=rho_high)
series_df = time_series_from_dist(hcbm_mats[0], dist="normal")
# Plot it
series_df.cumsum().plot(legend=None)
plt.show()
Research Notebook
The following research notebook can be used to better understand the Hierarchical Correlation Block Model.
Hierarchical Correlation Block Model