MDI, MDA, and SFI
Note
Underlying Literature
The following sources describe this method in more detail:
-
Advances in Financial Machine Learning, Chapter 8 by Marcos Lopez de Prado.
“Backtesting is not a research tool. Feature importance is.” (Lopez de Prado)
3 Algorithms for Feature Importance
The book describes three methods to get importance scores:
-
Mean Decrease Impurity (MDI): This score can be obtained from tree-based classifiers and corresponds to sklearn’s feature_importances attribute. MDI uses in-sample (IS) performance to estimate feature importance.
-
Mean Decrease Accuracy (MDA): This method can be applied to any classifier, not only tree based. MDA uses out-of-sample (OOS) performance in order to estimate feature importance.
-
Single Feature Importance (SFI): MDA and MDI feature suffer from substitution effects. If two features are highly correlated, one of them will be considered as important while the other one will be redundant. SFI is a OOS feature importance estimator which doesn’t suffer from substitution effects because it estimates each feature importance separately.
Implementation
- mean_decrease_impurity(model, feature_names, clustered_subsets=None)
-
Advances in Financial Machine Learning, Snippet 8.2, page 115.
MDI Feature importance
Mean decrease impurity (MDI) is a fast, explanatory-importance (in-sample, IS) method specific to tree-based classifiers, like RF. At each node of each decision tree, the selected feature splits the subset it received in such a way that impurity is decreased. Therefore, we can derive for each decision tree how much of the overall impurity decrease can be assigned to each feature. And given that we have a forest of trees, we can average those values across all estimators and rank the features accordingly.
Tip: Masking effects take place when some features are systematically ignored by tree-based classifiers in favor of others. In order to avoid them, set max_features=int(1) when using sklearn’s RF class. In this way, only one random feature is considered per level.
Notes:
-
MDI cannot be generalized to other non-tree based classifiers
The procedure is obviously in-sample.
-
Every feature will have some importance, even if they have no predictive power whatsoever.
-
MDI has the nice property that feature importances add up to 1, and every feature importance is bounded between 0 and 1.
-
method does not address substitution effects in the presence of correlated features. MDI dilutes the importance of substitute features, because of their interchangeability: The importance of two identical features will be halved, as they are randomly chosen with equal probability.
-
Sklearn’s RandomForest class implements MDI as the default feature importance score. This choice is likely motivated by the ability to compute MDI on the fly, with minimum computational cost.
Clustered Feature Importance( Machine Learning for Asset Manager snippet 6.4 page 86) : Clustered MDI is the modified version of MDI (Mean Decreased Impurity). It is robust to substitution effect that takes place when two or more explanatory variables share a substantial amount of information (predictive power).CFI algorithm described by Dr Marcos Lopez de Prado in Clustered Feature Importance section of book Machine Learning for Asset Manager. Here instead of taking the importance of every feature, we consider the importance of every feature subsets, thus every feature receive the importance of subset it belongs to.
- Parameters:
-
-
model – (object): Trained tree based classifier.
-
feature_names – (list): Array of feature names.
-
clustered_subsets – (list) Feature clusters for Clustered Feature Importance (CFI). Default None will not apply CFI. Structure of the input must be a list of list/s i.e. a list containing the clusters/subsets of feature name/s inside a list. E.g- [[‘I_0’,’I_1’,’R_0’,’R_1’],[‘N_1’,’N_2’],[‘R_3’]]
-
- Returns:
-
(pd.DataFrame): Mean and standard deviation feature importance.
-
- mean_decrease_accuracy(model, X, y, cv_gen, clustered_subsets=None, sample_weight_train=None, sample_weight_score=None, scoring=<function log_loss>, require_proba=True, n_repeat=1)
-
Advances in Financial Machine Learning, Snippet 8.3, page 116-117.
MDA Feature Importance (averaged over different random seeds n_repeat times)
Mean decrease accuracy (MDA) is a slow, predictive-importance (out-of-sample, OOS) method. First, it fits a classifier; second, it derives its performance OOS according to some performance score (accuracy, negative log-loss, etc.); third, it permutates each column of the features matrix (X), one column at a time, deriving the performance OOS after each column’s permutation. The importance of a feature is a function of the loss in performance caused by its column’s permutation. Some relevant considerations include:
-
This method can be applied to any classifier, not only tree-based classifiers.
-
MDA is not limited to accuracy as the sole performance score. For example, in the context of meta-labeling applications, we may prefer to score a classifier with F1 rather than accuracy. That is one reason a better descriptive name would have been “permutation importance.” When the scoring function does not correspond to a metric space, MDA results should be used as a ranking.
-
Like MDI, the procedure is also susceptible to substitution effects in the presence of correlated features. Given two identical features, MDA always considers one to be redundant to the other. Unfortunately, MDA will make both features appear to be outright irrelevant, even if they are critical.
-
Unlike MDI, it is possible that MDA concludes that all features are unimportant. That is because MDA is based on OOS performance.
The CV must be purged and embargoed.
Clustered Feature Importance( Machine Learning for Asset Manager snippet 6.5 page 87) : Clustered MDA is the modified version of MDA (Mean Decreased Accuracy). It is robust to substitution effect that takes place when two or more explanatory variables share a substantial amount of information (predictive power).CFI algorithm described by Dr Marcos Lopez de Prado in Clustered Feature Importance (Presentation Slides) https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3517595. Instead of shuffling (permutating) all variables individually (like in MDA), we shuffle all variables in cluster together. Next, we follow all the rest of the steps as in MDA. It can used by simply specifying the clustered_subsets argument.
- Parameters:
-
-
model – (sklearn.Classifier): Any sklearn classifier.
-
X – (pd.DataFrame): Train set features.
-
y – (pd.DataFrame, np.array): Train set labels.
-
cv_gen – (cross_validation.PurgedKFold): Cross-validation object.
-
clustered_subsets – (list) Feature clusters for Clustered Feature Importance (CFI). Default None will not apply CFI. Structure of the input must be a list of list/s i.e. a list containing the clusters/subsets of feature name/s inside a list. E.g- [[‘I_0’,’I_1’,’R_0’,’R_1’],[‘N_1’,’N_2’],[‘R_3’]]
-
sample_weight_train – (np.array) Sample weights used to train the model for each record in the dataset.
-
sample_weight_score – (np.array) Sample weights used to evaluate the model quality.
-
scoring – (function): Scoring function used to determine importance.
-
require_proba – (bool): Boolean flag indicating that scoring function expects probabilities as input.
-
n_repeat – (int) Number of times to repeat MDA feature importance with different random seeds.
-
- Returns:
-
(pd.DataFrame): Mean and standard deviation of feature importance.
-
- single_feature_importance(clf, X, y, cv_gen, sample_weight_train=None, sample_weight_score=None, scoring=<function log_loss>, require_proba=True)
-
Advances in Financial Machine Learning, Snippet 8.4, page 118.
Implementation of SFI
Substitution effects can lead us to discard important features that happen to be redundant. This is not generally a problem in the context of prediction, but it could lead us to wrong conclusions when we are trying to understand, improve, or simplify a model. For this reason, the following single feature importance method can be a good complement to MDI and MDA.
Single feature importance (SFI) is a cross-section predictive-importance (out-of- sample) method. It computes the OOS performance score of each feature in isolation. A few considerations:
-
This method can be applied to any classifier, not only tree-based classifiers.
-
SFI is not limited to accuracy as the sole performance score.
-
Unlike MDI and MDA, no substitution effects take place, since only one feature is taken into consideration at a time.
-
Like MDA, it can conclude that all features are unimportant, because performance is evaluated via OOS CV.
The main limitation of SFI is that a classifier with two features can perform better than the bagging of two single-feature classifiers. For example, (1) feature B may be useful only in combination with feature A; or (2) feature B may be useful in explaining the splits from feature A, even if feature B alone is inaccurate. In other words, joint effects and hierarchical importance are lost in SFI. One alternative would be to compute the OOS performance score from subsets of features, but that calculation will become intractable as more features are considered.
- Parameters:
-
-
clf – (sklearn.Classifier): Any sklearn classifier.
-
X – (pd.DataFrame): Train set features.
-
y – (pd.DataFrame, np.array): Train set labels.
-
cv_gen – (cross_validation.PurgedKFold): Cross-validation object.
-
sample_weight_train – (np.array) Sample weights used to train the model for each record in the dataset.
-
sample_weight_score – (np.array) Sample weights used to evaluate the model quality.
-
scoring – (function): Scoring function used to determine importance.
-
require_proba – (bool): Boolean flag indicating that scoring function expects probabilities as input.
-
- Returns:
-
(pd.DataFrame): Mean and standard deviation of feature importance.
-
- plot_feature_importance(importance_df, oob_score, oos_score, save_fig=False, output_path=None)
-
Advances in Financial Machine Learning, Snippet 8.10, page 124.
Feature importance plotting function.
Plot feature importance.
- Parameters:
-
-
importance_df – (pd.DataFrame): Mean and standard deviation feature importance.
-
oob_score – (float): Out-of-bag score.
-
oos_score – (float): Out-of-sample (or cross-validation) score.
-
save_fig – (bool): Boolean flag to save figure to a file.
-
output_path – (str): If save_fig is True, path where figure should be saved.
-
- Returns:
-
(matplotlib.figure.Figure) The produced plot figure.
Example
An example showing how to use various feature importance functions:
>>> import numpy as np
>>> import pandas as pd
>>> import yfinance as yf
>>> from sklearn.tree import DecisionTreeClassifier
>>> from sklearn.ensemble import BaggingClassifier
>>> from sklearn.metrics import (
... roc_curve,
... accuracy_score,
... precision_score,
... recall_score,
... f1_score,
... log_loss,
... )
>>> # Import MlFinLab tools
>>> from mlfinlab.ensemble.sb_bagging import SequentiallyBootstrappedBaggingClassifier
>>> from mlfinlab.feature_importance.importance import (
... mean_decrease_impurity,
... mean_decrease_accuracy,
... single_feature_importance,
... plot_feature_importance,
... )
>>> from mlfinlab.cross_validation.cross_validation import PurgedKFold, ml_cross_val_score
>>> from mlfinlab.util.volatility import get_daily_vol
>>> from mlfinlab.filters.filters import cusum_filter
>>> from mlfinlab.labeling.labeling import add_vertical_barrier, get_events, get_bins
>>> # Fetch data from Yahoo Finance
>>> data = yf.download("SPY", start="2012-03-25", end="2013-12-09", progress=False)
>>> # Create moving averages
>>> fast_window = 50
>>> slow_window = 100
>>> data["fast_mavg"] = (
... data["Close"]
... .rolling(window=fast_window, min_periods=fast_window, center=False)
... .mean()
... )
>>> data["slow_mavg"] = (
... data["Close"]
... .rolling(window=slow_window, min_periods=slow_window, center=False)
... .mean()
... )
>>> # Compute sides
>>> data["side"] = np.nan
>>> long_signals = data["fast_mavg"] >= data["slow_mavg"]
>>> short_signals = data["fast_mavg"] < data["slow_mavg"]
>>> data.loc[long_signals, "side"] = 1
>>> data.loc[short_signals, "side"] = -1
>>> # Remove Look ahead bias by lagging the signal
>>> data["side"] = data["side"].shift(1)
>>> # Filter events using the CUSUM filter
>>> daily_vol = get_daily_vol(close=data["Close"], lookback=50)
>>> cusum_events = cusum_filter(data["Close"], threshold=daily_vol.mean() * 0.5)
>>> # Do triple-barrier labelling
>>> vertical_barriers = add_vertical_barrier(
... t_events=cusum_events, close=data["Close"], num_days=1
... )
>>> pt_sl = [1, 2]
>>> min_ret = 0.005
>>> triple_barrier_events = get_events(
... close=data["Close"],
... t_events=cusum_events,
... pt_sl=pt_sl,
... target=daily_vol,
... min_ret=min_ret,
... num_threads=1,
... vertical_barrier_times=vertical_barriers,
... side_prediction=data["side"],
... )
>>> labels = get_bins(triple_barrier_events, data["Close"])
>>> # Feature Engineering
>>> X = pd.DataFrame(index=data.index)
>>> # Volatility
>>> data["log_ret"] = np.log(data["Close"]).diff()
>>> X["volatility_50"] = (
... data["log_ret"].rolling(window=50, min_periods=50, center=False).std()
... )
>>> X["volatility_31"] = (
... data["log_ret"].rolling(window=31, min_periods=31, center=False).std()
... )
>>> X["volatility_15"] = (
... data["log_ret"].rolling(window=15, min_periods=15, center=False).std()
... )
>>> # Autocorrelation
>>> window_autocorr = 50
>>> X["autocorr_1"] = (
... data["log_ret"]
... .rolling(window=window_autocorr, min_periods=window_autocorr, center=False)
... .apply(lambda x: x.autocorr(lag=1), raw=False)
... )
>>> X["autocorr_2"] = (
... data["log_ret"]
... .rolling(window=window_autocorr, min_periods=window_autocorr, center=False)
... .apply(lambda x: x.autocorr(lag=2), raw=False)
... )
>>> X["autocorr_3"] = (
... data["log_ret"]
... .rolling(window=window_autocorr, min_periods=window_autocorr, center=False)
... .apply(lambda x: x.autocorr(lag=3), raw=False)
... )
>>> X["autocorr_4"] = (
... data["log_ret"]
... .rolling(window=window_autocorr, min_periods=window_autocorr, center=False)
... .apply(lambda x: x.autocorr(lag=4), raw=False)
... )
>>> X["autocorr_5"] = (
... data["log_ret"]
... .rolling(window=window_autocorr, min_periods=window_autocorr, center=False)
... .apply(lambda x: x.autocorr(lag=5), raw=False)
... )
>>> # Log-return momentum
>>> X["log_t1"] = data["log_ret"].shift(1)
>>> X["log_t2"] = data["log_ret"].shift(2)
>>> X["log_t3"] = data["log_ret"].shift(3)
>>> X["log_t4"] = data["log_ret"].shift(4)
>>> X["log_t5"] = data["log_ret"].shift(5)
>>> X.dropna(inplace=True)
>>> labels = labels.loc[
... X.index.min() : X.index.max(),
... ]
>>> triple_barrier_events = triple_barrier_events.loc[
... X.index.min() : X.index.max(),
... ]
>>> X = X.loc[labels.index]
>>> X_train = X # We'll use all examples in this particular case
>>> y_train = labels.loc[X_train.index, "bin"]
>>> # Create, fit and cross-validate the model
>>> base_estimator = DecisionTreeClassifier(
... class_weight="balanced",
... random_state=42,
... max_depth=3,
... criterion="entropy",
... min_samples_leaf=4,
... min_samples_split=3,
... max_features="auto",
... )
>>> clf = BaggingClassifier(
... n_estimators=452,
... n_jobs=-1,
... random_state=42,
... oob_score=True,
... base_estimator=base_estimator,
... )
>>> _ = clf.fit(X_train, y_train)
>>> cv_gen = PurgedKFold(
... n_splits=3,
... samples_info_sets=triple_barrier_events.loc[X_train.index].t1,
... pct_embargo=0.10,
... )
>>> cv_score_acc = ml_cross_val_score(
... clf,
... X_train,
... y_train,
... cv_gen,
... sample_weight_train=None,
... scoring=accuracy_score,
... require_proba=False,
... )
>>> cv_score_f1 = ml_cross_val_score(
... clf,
... X_train,
... y_train,
... cv_gen,
... sample_weight_train=None,
... scoring=f1_score,
... require_proba=False,
... )
>>> # Produce the MDI, MDA, SFI feature maps
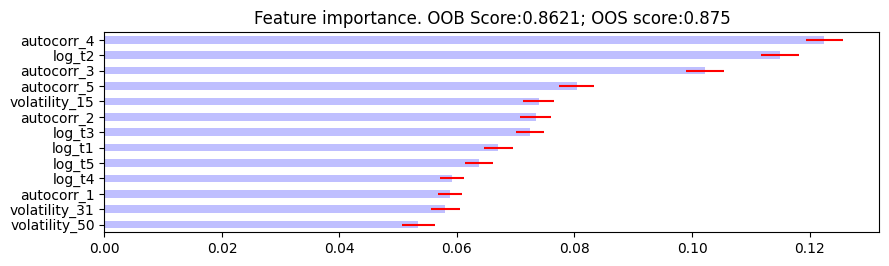
>>> mdi_feature_imp = mean_decrease_impurity(clf, X_train.columns)
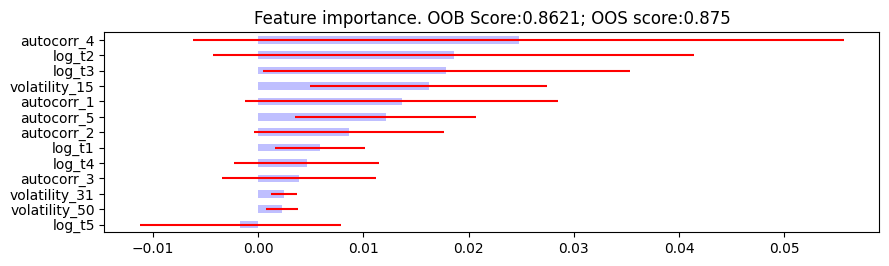
>>> mda_feature_imp = mean_decrease_accuracy(
... clf, X_train, y_train, cv_gen, scoring=log_loss
... )
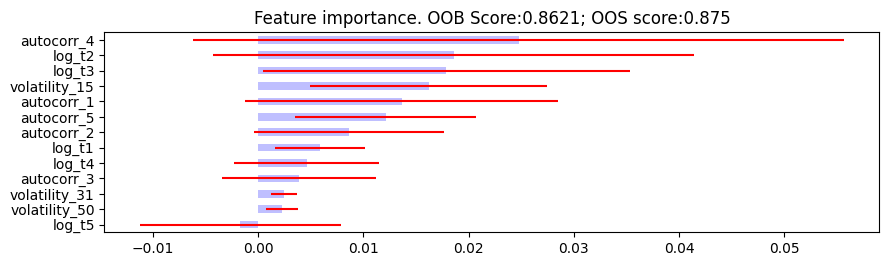
>>> sfi_feature_imp = single_feature_importance(
... clf, X_train, y_train, cv_gen, scoring=log_loss
... )
>>> # Plot
>>> plot_feature_importance(
... mdi_feature_imp, oob_score=clf.oob_score_, oos_score=cv_score_acc.mean()
... )
<...>
>>> plot_feature_importance(
... mda_feature_imp, oob_score=clf.oob_score_, oos_score=cv_score_acc.mean()
... )
<...>
>>> plot_feature_importance(
... sfi_feature_imp, oob_score=clf.oob_score_, oos_score=cv_score_acc.mean()
... )
<...>
The following are the resulting images from the MDI, MDA, and SFI feature importances respectively:
Research Notebook
-
Answering Questions on MDI, MDA, and SFI Feature Importance
Presentation Slides

Note
These slides are a collection of lectures so you need to do a bit of scrolling to find the correct sections.
pg 19-29: Feature Importance + Clustered Feature Importance.
pg 109: Feature Importance Analysis
pg 131: Feature Selection
pg 141-173: Clustered Feature Importance
pg 176-198: Shapley Values